Jeux Mathématiques et Logiques
document Gilles Hainry
http://www.univ-lemans.fr/~hainry/articles/loxonavi.html
ORTHODROMIE et LOXODROMIE
La ligne droite est le plus court chemin d'un point à
un autre ;
Qui n'a jamais entendu et fait sienne la maxime ci-dessus ? Et pourtant
...
La Terre
On appelle circonférence de la sphère la longueur
de n'importe lequel des plus grands cercles que l'on peut tracer sur sa surface
; en d'autres termes, la circonférence de la sphère est celle
du plus petit cercle au travers duquel on peut la faire passer ; on peut aisément
se représenter cette image en pensant au panier dans lequel passe un
ballon de basket-ball : ce panier est constitué d'un cercle dont la circonférence
minimale est celle du ballon.
La Terre, notre planète, a la forme d'un ellipsoïde de révolution
aplati, mais nous supposerons que c'est une sphère de 40 000 km de circonférence.
Le rayon de la terre est donc de 40 000 / (2.pi) soit environ 6 366 km ; c'est
la distance du centre O de la Terre à n'importe quel point de sa surface.
L'un des grands cercle joue un rôle particulier ; on l'appelle équateur
; il partage la Terre en deux : l'hémisphère Nord et l'hémisphère
Sud.
Tout cercle tracé sur la sphère et qui se trouve dans un plan
parallèle à celui qui contient l'équateur s'appelle un
parallèle.
Deux des parallèles (un dans l'hémisphère Nord et un dans
l'hémisphère Sud) sont réduits à un point (leur
rayon est nul) ; on les appelle pôles ; il y a donc un pôle Nord
et un pôle Sud.
La droite qui passe par les pôles est la perpendiculaire au plan équatorial
qui passe par le centre de la Terre ; on l'appelle axe des pôles
Les demi-cercles tracés sur la sphère qui ont pour extémités
les deux pôles sont des méridiens ; ce sont des moitiés
de grands cercles. L'un d'eux, celui qui passe par Greenwich (près de
Londres, en Angleterre), sert d'origine : c'est le méridien zéro
; il coupe l'équateur en un point G.
Latitude et longitude
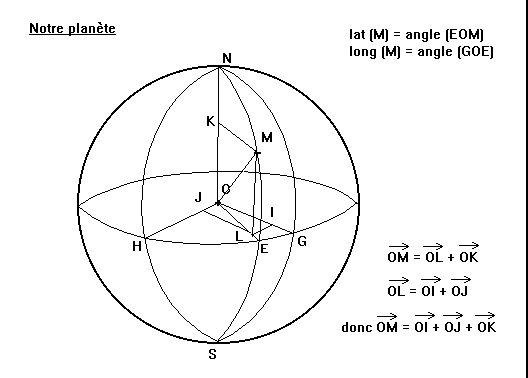
Tout point M de la Terre se trouve sur un méridien
qui coupe l'équateur en un point E ; le plus petit des deux angles (GOE)
est appelé longitude du point M ; si E est à l'Ouest de G, on
parle de longitude Ouest et celle-ci est comptée positivement ; dans
le cas contraire, il s'agit de longitude Est, et elle est comptée négativement.
 |
 |
|
|
L'angle (EOM) est appelé latitude du point M ; si
M est dans l'hémisphère Nord, elle est comptée positivement
et il s'agit d'une latitude Nord ; sinon, c'est une latitude Sud, qui sera comptée
négativement.
Il revient par exemple au même de dire que le port des Sables d'Olonne
se trouve à 46°45'N et 1°45'O ou bien que sa latitude est 46,75
et sa longitude 1,75 (on a converti les degrés/minutes en degrés
décimaux).
Le port de Fremantle en Australie, se trouve, lui, à environ 32°S
et 115°E, c'est à dire que sa latitude est approximativement -32
et sa longitude -115.
La coutume veut que les mesures soient effectuées en degrés et
minutes, et un arc de méridien joignant deux points dont les latitudes
diffèrent d'une minute s'appelle un mille marin ou plus simplement un
mille.
Les latitudes varient de -90° au pôle Sud à +90° au pôle
Nord en passant par 0° en tout point de l'équateur.
Les longitudes sont comprises entre -180° et +180°, ces deux extrèmes
représentant le même méridien (celui qui forme avec le méridien
Zéro un grand cercle).
Le mille marin
C'est, rappelons le de manière différente,
la longueur d'un arc de une minute sur un méridien (en assimilant arc
et angle au centre).
Puisque la longueur d'un méridien est de 20 000 km (un demi grand cercle),
et qu'un méridien représente un arc de 180°, on voit, puisqu'il
y a 60 minutes dans un degré que :
20 000 km = 180 * 60 milles
on a donc :
1 mille = 20 000 / 10 800 km
soit environ 1,852 km.
La vitesse d'un bateau ou d'un avion est généralement exprimée
en noeuds, le noeud équivalant à un mille marin par heure.
Ainsi par exemple, un bateau qui file 14 noeuds parcourt 14 milles marins à
l'heure ; sa vitesse exprimée différemment serait de 26 km/h environ
(14*1,852).
Notons que le mille marin est parfois appelé mille nautique ; il ne faudra
surtout pas le confondre avec le mile anglais qui est beaucoup plus court.
Coordonnées sphériques
Afin de repérer de manière cartésienne
les points de la Terre, imaginons l'espace muni d'un repère d'origine
O, d'axe des abscisses la droite (OG), d'axe des ordonnées la droite
(OH), d'axe des cotes la droite (ON), où O est le centre de la Terre,
G le point du méridien zéro qui se trouve sur l'équateur,
H le point de l'équateur de longitude 90°O et N le pôle Nord
; ces axes sont orientés de telle sorte que :
G a pour coordonnées (R ; 0 ; 0) ;
H a pour coordonnées (0 ; R ; 0) ;
N a pour coordonnées (0 ; 0 ; R) ;
où R représente la mesure du rayon de la Terre (qui dépend
bien sûr de l'unité choisie).
Pour obtenir les coordonnées d'un point M de la surface de la Terre,
connaissant ses latitude, notée lat(M), et longitude, notée long(M),
on projette le point M sur le plan (GOH) parallèlement à (ON)
; il s'agit en fait d'une projection orthogonale ; on obtient un point L tel
que OL = R . cos [ lat(M) ] .
on projette le point M sur l'axe (ON) pa rallèlement au plan (GOH), c'est
à dire à (OL) ; on obtient un point K de coordonnées (
0 ; 0 ; R . sin [ lat(M) ] ) .
on projette le point L sur l'axe (OG) orthogonalement, obtenant ainsi un point
I de coordonnées ( R . cos [ lat(M) ] . cos [ long(M) ] ; 0 ; 0) .
on projette le point L sur l'axe (OH) orthogonalement, obtenant ainsi un point
J de coordonnées ( 0 ; R . cos [ lat(M) ] . sin [ long(M) ] ; 0) .
L'abscisse de I, l'ordonnée de J et la cote de K sont respectivement
l'abscisse, l'ordonnée et la cote du point M, de telle sorte que l'on
a :
| R . cos [ lat(M) ] . cos [ long(M) ]
M | R . cos [ lat(M) ] . sin [ long(M) ]
| R . sin [ lat(M) ]
Rappelons que le théorème de Pythagore permet d'écrire
OM² = OL² + OK²
et
OL² = OI² + OJ²
et donc
OM² = OI² + OJ² + OK²
soit
OM² = (R . cos [ lat(M) ] . cos [ long(M) ] )² + (R . cos [ lat(M) ] . sin [ long(M) ] )² + (R . sin [ lat(M) ])²
= (R . cos [ lat(M) ] )² . [ (cos [ long(M) ] )² + ( sin [ long(M) ] )² ] + (R . sin [ lat(M) ])²
= (R . cos [ lat(M) ] )² + (R . sin [ lat(M) ])²
= R² . [ (cos [ lat(M) ] )² + (sin [ lat(M) ])² ]
= R²
ce qui est naturel puisque OM est un rayon de la Terre.
N.B. : on a utilisé dans cette démonstration la formule cos²(a)
+ sin²(a) = 1 vraie pour tout réel a.
Distance entre deux points
Soient A et B deux points de la surface de la Terre, leur
distance AB est par définition la mesure du segment [AB] ; cette mesure
ne dépend que de la différence de longitude entre Aet B ( que
l'on peut choisir comprise entre 0 et 180° ) et de leurs latitudes respectives
; on considèrera donc afin de simplifier l'écriture que A est
de longitude nulle, et l'on posera long = long(B)
On a donc :
| R . cos [ lat(B) ] . cos [ long ]
B | R . cos [ lat(B) ] . sin [ long ]
| R . sin [ lat(B) ]
et
| R . cos [ lat(A) ]
A | 0
| R . sin [ lat(A) ]
D'où AB² = ( R . cos [ lat(B) ] . cos [ long ] - R . cos [ lat(A) ] ) ² + ( R . cos [ lat(B) ] . sin [ long ] ) ²
+ (R . sin [ lat(B) ] - R . sin [ lat(A) ] ) ²
= 2 . R² . ( 1 - cos [ lat(A) ] . cos [ lat(B) ] . cos [ long ] - sin [ lat(A) ] . sin [ lat(B) ] )
soit :
AB = R . [ 2 . ( 1 - cos [ lat(A) ] . cos [ lat(B) ] . cos [ long ] - sin [ lat(A) ] . sin [ lat(B) ] ) ] ^ (1/2)
On doit cependant avoir à l'esprit que cette distance de A à B,
plus court chemin entre les deux points au sens euclidien du terme, nécessiterait
la percée d'un tunnel reliant A à B, ce qui n'est pas très
rationnel !
Distance orthodromique de deux points
Soient A et B deux points de la surface de la Terre ; la route la plus
courte pour aller du point A au point B est l'arc de grand cercle sous-tendu
par la corde [AB]. La longueur de cet arc, exprimée en milles, est la
mesure en minutes de l'angle (AOB) ; on l'appelle distance orthodromique de
A à B, et on la note ortho (A,B).
L'angle (AOB) est le double d'un angle dont le sinus est le quotient de AB/2
par R ; en effet, si l'on note T le milieu de [AB], le sinus de l'angle (AOT)
est le rapport du côté opposé et de l'hypoténuse
dans le triangle rectangle AOT, soit AT/OA où OA = R et AT = AB/2.
On a donc :
mes (A,B) = 2 arcsin ([ 2 . ( 1 - cos [ lat(A) ] . cos [ lat(B) ] . cos [ long ] - sin [ lat(A) ] . sin [ lat(B) ] ) ]^ (1 / 2) )
ou encore :
mes(A,B) = 2 arcsin ( [ ( 1 - cos [ lat(A) ] . cos [ lat(B) ] . cos [ long ] - sin [ lat(A) ] . sin [ lat(B) ] ) / 2 ]^ (1/2) )
et, si l'on a choisi de " travailler " en degrés, en multipliant
par 60, on obtient :
ortho (A,B) = 120 arcsin ( [ ( 1 - cos [ lat(A) ] . cos [ lat(B) ] . cos [ long ] - sin [ lat(A) ] . sin [ lat(B) ] ) / 2 ] ^(1/2) )
Cette formule étant un peu lourde, du fait de la racine carrée,
on va la transformer en utilisant quelques artifices trigonométriques.
On rappelle que cos ( 2 . u ) = 1 - 2 sin² ( u )
On a donc cos ( 2 . arcsin ( k ) ) = 1 - 2 . sin² ( arcsin ( k ) )
= 1 - 2 . k²
D'où 2 . arcsin ( k ) = arccos ( 1 - 2 . k² )
On en déduit que la distance orthodromique de A à B s'écrit
sous la forme simplifiée :
ortho (A,B) = 60 arccos ( cos [ lat(A) ] . cos [ lat(B) ] . cos [ long ] + sin [ lat(A) ] . sin [ lat(B) ] )
C'est d'ailleurs sous cette forme qu'on la trouve dans la plupart des ouvrages
de navigation.
Notons que le calcul est, de nos jours, grandement facilité par l'usage
d'une petite calculatrice scientifique dotée des fonctions trigonométriques
et des fonctions trigonométriques inverses ; la fonction arccos (respectivement
arcsin ou arctan) s'obtient le plus souvent en combinant les touches INV et
COS (respectivement INV et SIN ou INV et TAN). Nous nous permettons d'insister
sur la nécessité d'utiliser la machine en " mode degré
" et de veiller à la conversion des degrés et minutes en
degrés décimaux.
Distance orthodromique de Dunedin à Iquique
Le port de Dunedin en Nouvelle Zélande se trouve à environ
45° de latitude Sud et 170° de longitude Est.
Le port d' Iquique au nord du Chili se situe environ à 20° de latitude
Sud et 70° de longitude Ouest.
On a ainsi lat ( Dunedin ) = - 45 et long ( Dunedin ) = - 170
de même, lat ( Iquique ) = - 20 et long ( Iquique ) = 70
La différence de longitude 70 - (-170 ) = 240 sera remplacée par
120 ( 360°- 240° = 120° ) car il n'y a pas de raison de tourner
autour de la Terre en suivant le plus grand des deux arcs de grand cercle passant
par les deux ports.
On est ainsi amené à considérer deux points A et B tels
que
lat ( A ) = - 45 et long ( A ) = 0
lat ( B ) = - 20 et long ( B ) = 120 = long
On a alors
ortho (A,B) = 60 arccos ( cos [ - 45 ] . cos [ - 20 ] . cos [ 120 ] + sin [ - 45 ] . sin [ - 20 ] )
= 60 arccos ( - 0.0904 )
= 60 . 95,19
= 5 711 milles
La distance orthodromique de Dunedin à Iquique est donc de 5 711 milles
ou encore 10 463 km ; notons que c'est la mesure de la route la plus courte
entre les deux ports, mais qu'un tunnel en ligne droite les mettrait à
9 400 km l'un de l'autre : En effet 5 711 milles représentent un angle
au centre de 5 711 minutes, soit 95,18° et
AB = 2. R . sin ( 95,18 / 2 ) = 2 R sin ( 47,59 ) = 1,4767 . R avec R = 6 366
km, d'où AB = 9 400 km.
La projection de Mercator
Une manière commode de représenter la surface
du globe sur une surface plane consiste à utiliser la projection dite
de Mercator :
Sur un cylindre tangent à la Terre le long de l'équateur, et qui
a donc pour axe l'axe des pôles, on projette chaque point de la surface
de la Terre perpendiculairement à cet axe ; de façon plus précise,
disons que l'on choisit comme image d'un point M de la Terre le plus proche
de M des deux points d'intersection de la perpendiculaire à l'axe passant
par M et du cylindre. Les deux pôles posent évidemment problème
et ont chacun pour image un cercle entier du cylindre parallèle à
l'équateur, distant de R de celui-ci.
En coupant le cylindre par une perpendiculaire à l'équateur, puis
en le déroulant, la Terre se trouve représentée par un
grand rectangle qu'on appelle une carte géographique.
Un avantage évident de cette représentation est que les parallèles
sont des droites parallèles à l'équateur et aux grands
côtés du rectangle, tandis que les méridiens sont des droites
perpendiculaires à l'équateur, parallèles aux petits côtés
du rectangle.
Un inconvénient majeur de cette représentation est que les distances
ne sont pas respectées et que la route orthodromique, c'est à
dire la plus courte n'est jamais une droite, sauf pour deux points situés
sur un même méridien.
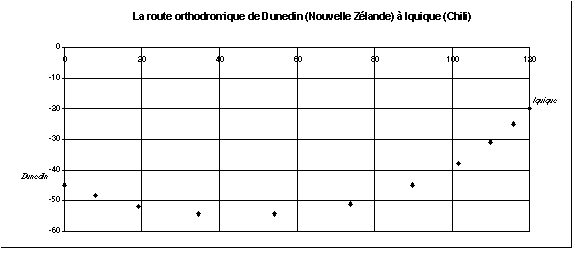
Le diagramme ci dessous montre la route orthodromique de Dunedin à Iquique
sur une carte de Mercator.
| |
 |
 |
|
Les onze points permettent de se faire une idée de
la route ; la distance entre deux points consécutifs n'est pas constante,
mais, le sixième point ( latitude : -51,06° ; différence de
longitude : 73,75° avec Dunedin, 46,25° avec Iquique ) est au milieu
de la route
Certains seront sans doute surpris que cette route parte
d'abord vers le sud-est (la latitude décroît, la longitude croît),
puis s'infléchisse et se termine en direction du nord-est (latitude et
longitude croissent simultanément)...
Distance orthodromique de deux points du cercle polaire
Pour mieux comprendre le phénomène observé
dans le précédent paragraphe, il suffit de penser à la
route orthodromique entre deux points A et B situés aux deux extrémités
d'un diamètre du cercle polaire arctique (66,567° de latitude Nord
pour les deux points et 180° de différence de longitude) ; cette
route passe par le pôle Nord, c'est à dire qu'elle commence plein
nord et se termine plein sud ; en effet, le grand cercle passant par ces deux
points passe aussi par les deux pôles.
Plus précisément, la mesure de la route orthodromique entre ces
deux points est de 60 * ( 180 - 2 * 66,567 ) milles, soit 2812 milles ; en effet,
il suffit de mesurer en minutes l'angle au centre correspondant, c'est à
dire de déduire d'un angle plat (180°) deux fois la latitude de A
ou B.
On retrouve d'ailleurs ce résultat avec la formule établie plus
haut :
ortho (A,B) = 60 arccos ( cos [ lat(A) ] . cos [ lat(B) ] . cos [ long ] + sin [ lat(A) ] . sin [ lat(B) ] )
avec cos [ long ] = cos (180) = - 1 et lat(A) = lat(B)
d'où ortho (A,B) = 60 arccos ( - cos²[ lat(A) ] + sin²[ lat(A) ] )
= 60 arccos ( - cos [ 2 lat(A) ] )
= 60 arccos ( cos [ 180 - 2 lat(A) ] )
= 60 * [ 180 - 2 lat(A) ]
= 60 * [ 180 - 2 * 66,567 ]
comme souhaité.
Par contre, si l'on allait d'un point à l'autre en suivant le cercle
polaire, toujours plein est ou toujours plein ouest, on parcourrait une distance
de pi fois le rayon de ce cercle, soit pi * cos ( 66,567 ) * R ; comme le rayon
de la Terre est R = 180 * 60 / pi (soit 3437 milles), cela ferait 10 800 cos
( 66,567 ) = 4 295 milles.
Notons que la distance euclidienne entre ces points A et B est bien sûr
inférieure à la distance orthodromique, puisqu'elle est :
AB = R . [ 2 . ( 1 - cos [ lat(A) ] . cos [ lat(B) ] . cos [ long ] - sin [ lat(A) ] . sin [ lat(B) ] ) ] ^(1/2)
= R . [ 2 . ( 1 + cos²[ lat(A) ] - sin²[ lat(A) ] ) ] ^(1/2)
= R . [ 2 . ( cos²[ lat(A) ] + sin²[ lat(A) ] + cos²[ lat(A) ] - sin²[ lat(A) ] ) ] ^(1/2)
= R . [ 4 cos²[ lat(A) ]^(1/2)
= 2 R cos [ lat(A) ] puisque lat(A) possède un cosinus positif
= 2 734 milles.
mais, cela ne correspond à rien sur la carte, puisque
seules les extrémités du segment [AB] sont sur la Terre, ses autres
points étant à l'intérieur de la Terre...
Route loxodromique
On a certes du mal à imaginer que la ligne droite
tracée sur une carte de Mercator ne représente pas la route optimale
pour relier deux points lui appartenant ; nous avons vu plus haut que la route
orthodromique de Dunedin à Iquique, qui, rappelons le, est la plus courte,
n'est pas le segment joignant les deux ports sur cette carte.
La route qui relie deux points de la Terre en suivant le segment qui les joint
sur une carte de Mercator est dite loxodromique ; il faudra se rappeler que,
si cette route peut se mesurer, cette mesure n'est pas une distance (au sens
mathématique du terme) et que cette route n'est pas le plus court chemin
pour relier ces deux points.
Cependant, une route loxodromique est simple à tracer sur une carte (à
la règle) et l'on peut très facilement trouver les latitudes et
longitudes des points qui se trouvent sur cette route.
Une telle route présente l'avantage de couper chaque méridien
selon un angle constant ; cela permet par exemple au navigateur de conserver
le même cap durant tout le trajet pour la suivre, ce qui -on l'a vu- n'est
pas le cas sur une route orthodromique.
Il y a en fait deux sortes de routes loxodromiques :
- celles qui joignent deux points situés à la même latitude
; elles sont portées par les parallèles et constituent donc sur
la Terre des arcs de cercle.
- celles qui joignent deux points A et B de latitudes différentes ; elles
constituent des arcs de courbes joignant les pôles puisque les bords supérieur
et inférieur d'une carte de Mercator (1) représentent respectivement
le pôle Nord et le pôle Sud ; ces courbes sont des demi-cercles
(2) dans le cas particulier où les deux points ont même longitude
et seulement dans ce cas.
Remarques : (1) il faut ici imaginer plusieurs cartes de Mercator côte
à côte, car la " loxodromie " s'enroulera en spirale
plusieurs fois autour de la Terre avant de rejoindre les pôles si la pente
de la droite (AB) est faible.
(2) dans ce cas, le demi-cercle en question est naturellement un méridien.
Il est encore plus troublant que la route la plus courte ne soit pas celle consistant
à suivre le parallèle (du bon côté) lorsque les points
ont la même latitude ; nous avons pourtant fait les calculs et apporté
la preuve de ce résultat dans le cas de deux points symétriques
par rapport à l'axe des pôles et situés sur le cercle polaire
arctique...
Des Sables à l'île Sable
Nous pouvons aussi citer un exemple qui nous a été
malicieusement donné par notre collègue Edouard Poulain, Maître
de Conférences à l'Université du Maine et... marin :
La latitude des Sables d'Olonne, en Vendée, 46,5° N environ, est
presque la même que celle du Cap Canso, au nord de l'île Sable,
de l'autre côté de l'Atlantique, en Nouvelle Ecosse.
La longitude du Cap Canso est sensiblement égale à 61,75°
W ; celle des Sables d'Olonne étant proche de 1,75° W on a donc une
différence de longitude de 60°.
La distance orthodromique entre les deux points que l'on notera encore A et
B est :
ortho (A,B) = 60 arccos ( cos²[ 46,5 ] . cos [ 60 ] + sin²[ 46,5 ] )
= 2 416 milles
La mesure de la route loxodromique de A à B est
loxo (A,B) = 60 * 60 * cos (46,5)
= 2 478 milles
Bien que minime, la différence est tout de même sensible puisque
l'on peut observer que la route loxodromique est de 2,5% plus longue que la
route orthodromique.
Le 45° parallèle
Le tableau ci-après montre l'évolution des
mesures relatives des routes orthodromique et loxodromique reliant deux points
du 45ème parallèle (Nord par exemple) en fonction de la différence
de longitude entre ces points ; nous avons, à titre indicatif, ajouté
la distance euclidienne AB notée ici seg(A,B).
Nous avons choisi d'exprimer dans ce tableau les résultats
en kilomètres, ce qui ne change rien aux différences relatives,
afin que chacun puisse remarquer que pour une différence de longitude
de 180°, la route orthodromique (qui passe par le pôle Nord) est un
quart de grand cercle.
On peut voir que la différence relative entre les deux mesures ortho(A,B)
et loxo(A,B) croît sur l'intervalle [0°;180°] pour atteindre un
maximum de 41,4%, ce qui est loin d'être négligeable.
Route loxodromique simple (points ayant même latitude)
Il est relativement simple de calculer la mesure de la route
loxodromique reliant A à B lorsque ces deux points ont la même
latitude ; il suffit en effet de mesurer un arc de parallèle.
On a lat(A) = lat(B) ; A et B se trouvent sur un cercle de centre Q (Q est confondu
avec O si lat(A) = 0) ; le rayon [QA] de ce cercle est R * cos [ lat(A)] et
l'angle (AQB) a pour mesure la différence de longitude entre A et B.
L'arc de cercle (parallèle) joignant A et B a donc pour mesure cos [
lat(A)] fois l'arc d'équateur joignant deux points dont la différence
de longitude serait la même.
On en déduit que
loxo (A,B) = 60 . long . cos [ lat(A) ] lorsque lat(A) = lat (B)
Nous avons d'ailleurs déjà utilisé cette formule.
C'est malheureusement plus compliqué lorsque les deux points ont des
latitudes différentes, c'est à dire lorsqu'ils ne se trouvent
pas situés sur un même parallèle...
Route loxodromique (cas général)
Notons tout de même qu'il existe encore un cas particulièrement
simple : celui où les deux point appartiennent au même méridien
; en effet, un méridien étant un demi grand cercle, la route orthodromique
se confond dans ce cas avec la route loxodromique et l'on a alors
loxo (A,B) = ortho (A,B)
= 60 arccos ( cos [ lat(A) ] . cos [ lat(B) ] + sin [ lat(A) ] . sin [ lat(B) ] )
= 60 arccos ( cos [ lat(A) - lat(B) ] )
= 60 . abs ( [ lat(A) ] - lat(B) ] )
lorsque la différence de longitude est nulle, c'est à dire si long = 0
Résumons :
loxo (A,B) = ortho (A,B) = 60 . abs ( [ lat(A) ] - lat(B) ] ) lorsque long = 0
où abs ( nombre ) est la valeur absolue de nombre.
Venons en maintenant au cas général :
A et B sont deux points de la surface de la Terre ; on considère afin
de simplifier l'écriture que A est de longitude nulle, et l'on posera
long = long(B)
On a donc :
| R . cos [ lat(B) ] . cos [ long ]
B | R . cos [ lat(B) ] . sin [ long ]
| R . sin [ lat(B) ]
et
| R . cos [ lat(A) ]
A | 0
| R . sin [ lat(A) ]
La route loxodromique de A à B est l'arc qui correspond au segment [AB]
tracé sur la carte de Mercator ; c'est donc l'ensemble des points M de
latitude
lat(M) = lat(A) + t . [ lat(B) - lat(A) ]
et ayant avec A une différence de longitude
long(M) = t . long pour t variant de 0 à 1.
Pour t = 0 le point M est en A ; pour t = 1 il est confondu avec B.
On obtient ainsi une paramètrisation de l'arc AB sous la forme d'une
fonction de t :
| R . cos [ lat(A) + t . [ lat(B) - lat(A) ] ] . cos [ t . long ]
f (t) | R . cos [ lat(A) + t . [ lat(B) - lat(A) ] ] . sin [ t . long ]
| R . sin [ lat(A) + t . [ lat(B) - lat(A) ] ]
La mesure de la longueur de l'arc AB est alors donnée, en degrés
, par l'intégrale sur l'intervalle [ 0 ; 1 ] de la norme de la dérivée
de f ( nous n'insisterons pas sur la démonstration de cette formule et
renvoyons les lecteurs intéressés au tome 3 du cours de mathématiques
de Lelong-Ferrand et Arnaudiès chez Dunod Université).
Soit

(en degrés)
Il suffit alors de multiplier le résultat par 60 pour exprimer cette
mesure en milles. D'où
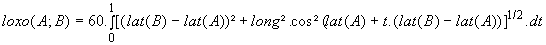
Merci à:
service maintenu par
Gilles HAINRY, agrégé
de mathématiques,
Université du Maine
I.U.T. Techniques de Commercialisation
53000 LAVAL
(France)
Centre
de Pilotage Choletais - Aérodrome - 49300 CHOLET - Tel/Fax : 02 41 58
76 61
retour pilotage.choletais@free.fr









![]()